Re-Envisioning the Mathematics Teaching Practices as the Statistics Teaching Practices

Natasha E. Gerstenschlager
In 2014, the Mathematics Teaching Practices (MTPs) were released by the National Council of Teachers of Mathematics in Principles to Actions: Ensuring Mathematical Success for All. These eight practices are described as practices based in research that ensure students receive quality mathematics instruction.
As a mathematics teacher educator, I promote these practices and use them in my content classrooms for pre- and in-service teachers. However, as I reflected on how I would use these in my statistics content course for secondary mathematics teachers, I noticed many of the practices do not look the same when implemented in a statistics classroom. This made me wonder how these practices might look differently when the focus is on statistics.
After reflecting on documents such as the Statistical Education of Teachers, Guidelines for Assessment and Instruction in Statistics Education, and Common Core State Standards for Mathematics, I re-envisioned the eight MTPs as the eight Statistics Teaching Practices (STPs). It is important to note that although the practice title for each STP appears similar to the original (with minor words being changed in some cases), the description underneath demonstrates how the meaning of each STP is different.
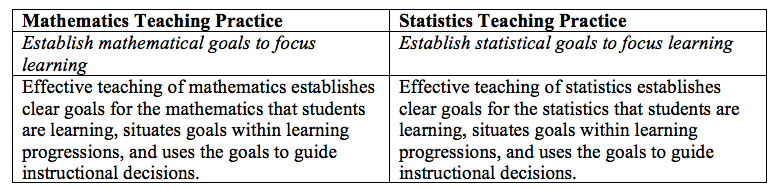
Note: It is important that we have learning goals for our students at all levels: task or lesson, unit, and course. For simplicity, I chose only to focus on establishing goals for tasks.
According to Dung Tran and Hollylynne Lee in “Considerations for Design and Implementation of Statistics Tasks,” establishing a statistical goal is a key feature of a statistical task and essentially different from a mathematical task goal. Mathematical tasks focus on conceptual understanding of procedures, computations, algorithms, and mathematical concepts. We often see mathematical goals in statistics lessons when students use algorithms, create graphs, and calculate descriptive statistics. Statistical tasks should focus on how to use these mathematical artifacts to make statistical decisions in regard to a statistical question. For example, how can the results from the algorithm or what we can glean from this graph help us answer a statistical question or make a statistical decision?
As such, establishing statistical goals requires that we think strategically about the statistics trajectory we have set for our students, how mathematics supports this trajectory, and how the statistics in the task engages students in the statistical problem-solving process.
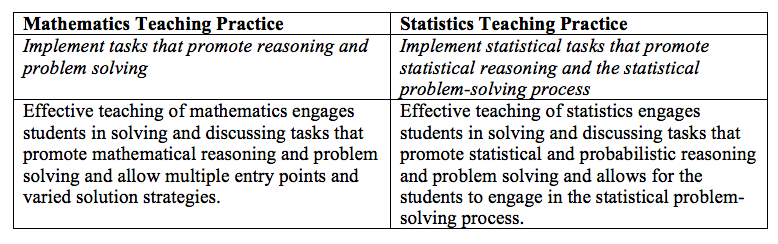
The key difference between these two practices is the shift from promoting mathematical reasoning to statistical reasoning. These two types of reasoning require different types of thinking, and, as such, are fostered in different ways.
Statistical thinking has been defined by Ronald Snee in his The American Statistician article titled “Statistical Thinking and Its Contribution to Quality” as “thought processes, which recognize that variation is all around us and present in everything we do, all work is a series of interconnected processes, and identifying, characterizing, quantifying, controlling, and reducing variation provide opportunities for improvement.”
To develop statistical thinking, Lee and Tran describe seven statistical habits of mind, some of which are considering the context of the data; anticipating, looking for, and describing variation; and being skeptical throughout a statistical investigation. Developing these habits of mind throughout the statistical problem-solving process, as Lee and Tran suggest, provides students with opportunities to see how statistical thinking is different from mathematical thinking. Additionally, it allows students to use mathematical and probabilistic reasoning when making statistical decisions.
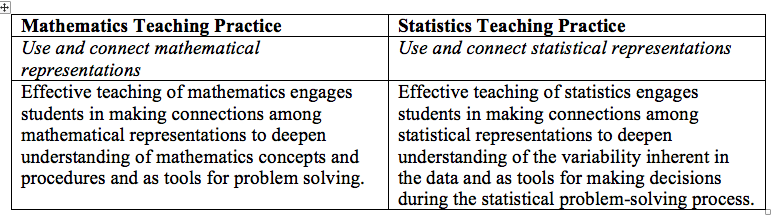
Many would agree that mathematical representations often appear in statistics. However, the difference in these two teaching practices is in how the representations are used and in what the goal is for using them. Students in a statistics classroom must not only be able to create the graphical representation, but also select the most appropriate graphical representation for a particular data set that effectively portrays or describes the variability in the data and helps in answering the statistical question at hand.
The selection of an appropriate statistical representation is not a trivial matter, as portraying the data appropriately assists in making sound statistical decisions. When teaching statistics, we should introduce students to a variety of representations and develop students’ ability to determine effective representations based on varying data sets.
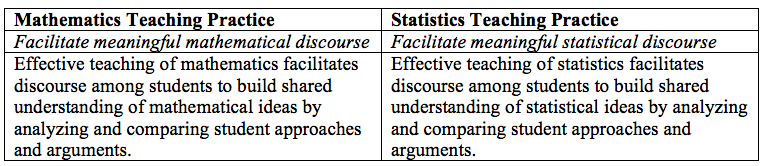
The difference between these practices is evident in how the Statistical Education of Teachers document describes the Standard for Mathematical Practice (SMP) of “constructing viable arguments and critique the reasoning of others” in the statistics classroom. Specifically, for this SMP, students in the statistics classroom should be able to “compare the plausibility of alternative conclusions and distinguish correct statistical reasoning from that which is flawed.”
Facilitating a statistical discussion requires that we foster a healthy sense of skepticism. One similarity between the MTP and STP is that many of the strategies used in promoting the MTP are still useful when addressing the STP. For example, the five practices for orchestrating a mathematical discussion, detailed by Margaret Schwan Smith and Mary Kay Stein in 5 Practices for Orchestrating Productive Mathematics Discussions, are still necessary when orchestrating statistical discussions and can help students leverage a deeper understanding of the statistics content.
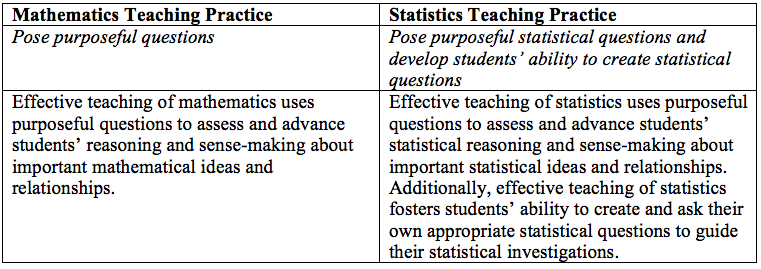
This MTP focuses on using purposeful questioning from the teacher to develop students’ thinking and understanding of a particular mathematics topic. This type of questioning is equally as important in statistics (justifying why the first sentence of the STP is basically the same); however, statistical questioning in regard to the statistical problem-solving process is a unique trait of statistics. We have to develop students’ ability to ask appropriate statistical questions, and this skill should become more refined as students progress through a statistics and probability learning progression. That is, at first, students will likely need help from us to develop and create appropriate statistical questions. Initially, we may even need to provide statistical questions for the students to explore. However, as their understanding of statistics develops, students should become more aware of what makes a question statistical and be able to create their own statistical questions to guide their investigations.
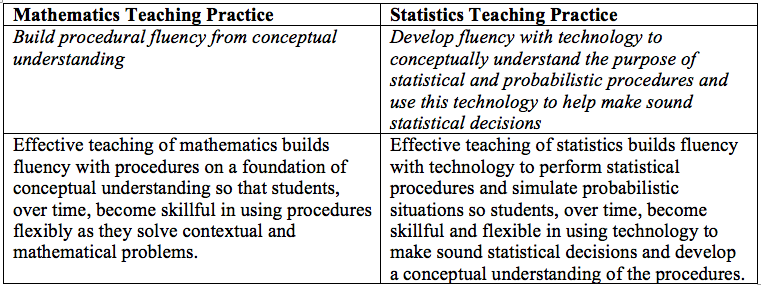
In mathematics, there exist many procedures we want our students to understand conceptually and be able to execute efficiently. As an example, our students need to be able to multiply fractions fluently and justify why the standard algorithm for multiplying fractions is what it is.
This focus on procedural fluency developed from conceptual understanding allows students to not have to simply memorize facts and formula. It frees them to develop deeper understanding of why and how things work mathematically.
Although this is extremely important in both mathematics and statistics, this type of procedural fluency should not be a specific goal in statistics. Though students should understand how to compute statistics by hand (e.g., mean, median, standard deviation, mean absolute deviation) and do so efficiently, these procedures are inherently mathematical. On the other hand, a goal of statistics instruction is for students to interpret statistics in context and make sound statistical decisions based on the mathematical and statistical procedures we have used. As such, students should be able to quickly move from calculating statistics, performing procedures, and simulating probabilistic situations by hand to fluently using technology to do these processes for them.
Various technologies exist that can be used in the classroom (e.g., TI calculators, CODAP, Tinkerplots), and we should consider which is most effective for our students and the statistical goals set forth for the particular unit. Additionally, we should focus students’ learning on making sense of technological output for the purpose of making statistical decisions, and, if necessary, making changes to their technological output (e.g., asking the technology to produce a different statistic or representation) to compare various approaches. Moreover, we should develop students’ ability to translate what they learn from tactile probability simulations into larger simulations using technology. Given the power of current technology, this latter focus is especially important as students learn randomization approaches during units on statistical inference.
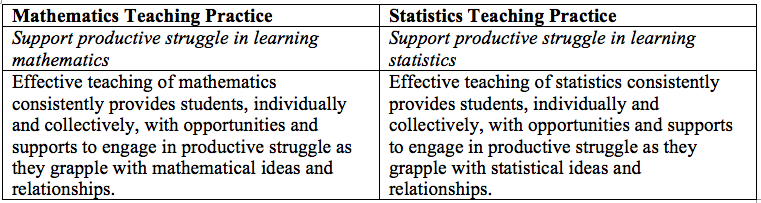
Although these teaching practices do not seem to be very different, the main difference comes from the nature of statistics. That is, the presence of variability within statistics and the subjectivity that can appear in the statistical decision-making process is different than the nature of mathematics. As such, students of mathematics are regularly frustrated when they learn statistics due to these aspects.
Specific examples of frustrations for students in the statistics classroom include conceptualizing the different kinds of variability found in a data set; choosing a most appropriate statistic to describe a data set, interpretations, and representations; and using statistical terms and definitions appropriately and with precision (e.g., using “significant” only when it is appropriate).
Therefore, it is imperative that we consider ways to scaffold students when they do struggle with these ideas in a way that helps them progress with the content. Scaffolding suggestions from the mathematics education literature are still relevant for the teaching of statistics and can be used as guides.
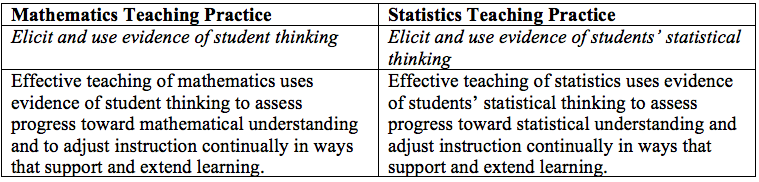
The primary difference between these two practices is in what types of thinking are elicited in the classroom. In the statistics classroom, teachers should focus on eliciting statistical thinking, not mathematical thinking. For example, when students are analyzing a data set, they may decide to calculate various statistics to help them describe the data. Students who share their mathematical thinking would present how they found those statistics (e.g., “I added all the data points and divided by how many data points there were.”). In contrast, students who share their statistical thinking would present why they decided to calculate a certain statistic in lieu of another or how the various statistics tell us different information about the data set. Engaging in this practice requires that we know what statistical thinking needs to be elicited to achieve the learning goal for the lesson.
The MTPs represent eight research-based teaching practices that engage students in rigorous and robust mathematics. Similarly, the STPs presented summarize instructional practices we can use in our classrooms to engage students in rigorous and robust mathematics. Being explicit in describing what these STPs are and detailing how they are different from and similar to the MTPs is important, as it helps us understand how the statistics classroom looks different than the mathematics classroom.